
과대적합(overfitting)과 과소적합(underfitting)
- 과대적합(overfitting)
과대적합(overfitting)은 모델이 훈련 데이터를 과하게 학습한 것을 의미합니다. 너무 훈련 데이터에 학습이 잘 되 있으면 훈련 데이터 이외의 학습되지 않은 데이터가 들어오면 분류하지 못하게 됩니다.
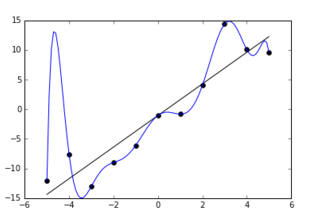
위의 그림처럼 파란 선의 모델이 훈련데이터를 정확히 다 거치며 과대적합되고 있습니다. 이는 모델의 복잡도가 필요 이상으로 높기 때문에 이를 방지하기 위해 규제를 통해 모델의 복잡도를 낮추어 간단하게 해주어야 합니다.
모델을 단순하게 하고 과대적합의 위험을 감수시키기 위해 모델에 제약을 가하는 것을 규제라고 합니다. 학습하는 동안 적용할 규제의 양은 하이퍼파라미터(hyperparameter)가 결정합니다. 하이퍼파라미터는 학습 알고리즘으로부터 영향을 받지 않으며 훈련 전에 미리 지정되어 훈련하는 동안에는 상수로 남아있게 됩니다. 하이퍼파라미터 값을 너무 높이면 과소적합의 문제가 발생할 수도 있으므로 적절하게 설정하는 것이 좋겠습니다.
- 과소적합(underfitting)
과소적합은 모델이 너무 단순해서 데이터의 내재된 구조를 학습하지 못할 때 발생합니다. 과소적합을 해결하기 위해서는 파라미터가 더 많은 복잡한 모델을 선택하고 규제 하이퍼파라미터 값을 줄여 모델의 제약을 줄여줍니다. 그리고 조기종료 시점을 overfitting이 되기 전의 시점까지 충분히 학습시켜주어 최상의 결과가 나올 때 까지 학습해줍니다.
다중 회귀(multiple regression)
단순 선형 회귀보다 고려해야 하는 변수가 많을 때 다중 회귀를 사용합니다. 예를 들어 부동산 집값을 예상할 때 주변에 필요한 시설이 있는지 교통은 편리한지 얼마나 오래되었는지 등 여러가지 요소들의 영향을 받습니다.

위의 그림처럼 특성이 2개면 선형 회귀는 평면을 학습합니다. 특성이 3개 이상부터는 특성 공간을 그리거나 상상할 수 없습니다. 특성이 많은 고차원에서는 선형 회귀가 매우 복잡한 모델을 표현할 수 있습니다.
특성 공학(feature engineering)의 정의
Feature Engineering은 모델 정확도를 높이기 위해서 주어진 데이터를 예측 모델의 문제를 잘 표현할 수 있는 features로 변형시키는 과정입니다. '머신러닝 알고리즘을 작동하기 위해 데이터의 도메인 지식을 활용해 feature를 만드는 과정'이라고 할 수도 있습니다. Feature Engineering에 대한 자세한 내용은 추후에 따로 정리하도록 하겠습니다.
Ridge Regression (릿지 회귀, L2 Regression)

릿지 회귀식을 보면 잔자제곱합(RSS : residual sum of squares) + 패널티 항(베타 값)의 합으로 이루어져있습니다. 릿지회귀의 패널티항은 파라미터의 제곱을 더해준 것입니다. 이것은 미분이 가능해 Gradient Descent 최적화가 가능하고, 파라미터의 크기가 작은 것보다 큰 것을 더 빠른 속도로 줄여줍니다. 다시 말하면 λ(람다)가 크면 클수록 리지회귀의 계수 추정치는 0에 가까워 지는 것입니다. (λ = 0 일 때는 패널티 항은 효과가 없고, 따라서 리지 회귀(ridge regression)은 최소제곱추정치를 생성) 즉, λ(람다)가 패널티를 얼마나 부과하는가를 조절하는 조절버튼이라고 생각하면 되겠습니다.
릿지회귀의 β0^2+β1^2의 제약조건인 원이 있습니다. 기존의 OLS(Ordinary Least Squares)가 아래에 보이는 제약조건까지 와야지 최적값이라고 할 수 있는 것입니다. 그렇다면 OLS가 제약조건까지 오기 위해서는 RSS(RSS : residual sum of squares) 크기를 키워주게 됩니다. bias가 약간의 희생은 하지만 variance를 줄이기 위해서 아래의 그림처럼 제약조건까지 오는 가장 작은 RSS를 고르면 되는 것 입니다.

Lasso Regression (라쏘 회귀, L1 Regression)

라쏘회귀는 릿지회귀와 비슷하게 생겼지만 패널티 항에 절대값의 합을 주었습니다.
라쏘는 제약조건이 절대값이라 아래의 그림처럼 마름모꼴의 형태로 나타납니다. 릿지회귀와 비슷하게 OLS의 RSS 값을 크게 늘려줍니다. 라쏘회귀의 경우 최적값은 모서리 부분에서 나타날 확률이 릿지에 비해 높아 몇몇 유의미하지 않은 변수들에 대해 계수를 0에 가깝게 추정해 주어 변수 선택 효과를 가져오게 됩니다. 라쏘회귀는 파라미터의 크기에 관계없이 같은 수준의 Regularization을 적용하기 때문에 작은 값의 파라미터를 0으로 만들어 해당 변수를 모델에서 삭제하고 따라서 모델을 단순하게 만들어주고 해석에 용이하게 만들어줍니다.


ridge, Lasso 참고 : https://rk1993.tistory.com/entry/Ridge-regression%EC%99%80-Lasso-regression-%EC%89%BD%EA%B2%8C-%EC%9D%B4%ED%95%B4%ED%95%98%EA%B8%B0







github 코드 첨부
https://github.com/erdnussretono/Polynomial_Ridge_Lasso/blob/main/multiple%20regression.ipynb
erdnussretono/Polynomial_Ridge_Lasso
Contribute to erdnussretono/Polynomial_Ridge_Lasso development by creating an account on GitHub.
github.com
- PolynomialFeature
- degree는 최고 차수를 지정합니다. default 값은 2 입니다.
- include_bias가 False이면 절편을 위한 특성을 추가하지 않습니다. sklearn 모델은 자동으로 절편에 추가된 항을 무시합니다.
'AI' 카테고리의 다른 글
| 손실함수(Loss Function)의 종류 (1) | 2021.07.20 |
|---|---|
| [머신러닝] 로지스틱 회귀(logistic regression) (0) | 2021.07.17 |
| [머신러닝] 선형회귀(Linear Regression) (0) | 2021.07.17 |
| KNN(K-Nearest Neighbors) 회귀(regression) (0) | 2021.07.17 |
| [데이터 전처리] titanic data 전처리 (0) | 2021.07.17 |